

User Controls
Vitalik Buterin's "Circle STARKs" the next leap in tech
-
2024-07-24 at 10:12 PM UTChttps://cointelegraph.com/news/vitalik-buterin-introduces-circle-starks-blockchain-efficiency
According to the post, traditional scalable transparent arguments of knowledge (STARKs) operate over 256-bit fields, which, while secure, are typically inefficient.
Circle STARKs leverage smaller fields, resulting in reduced computational costs, faster-proving speeds and more efficient gains, such as verifying 620,000 Poseidon2 hashes per second on an M3 laptop.
Buterin notes that previous STARK implementation made smaller fields “naturally compatible with verifying elliptic curve-based signatures” but “led to inefficiency” due to the large numbers involved.
Circle STARK security
Traditional small fields have limited possible values and can become exposed to brute-force attacks.
Circle STARKs counteract this vulnerability by performing multiple random checks and using extension fields, expanding the set of values that attackers need to guess.
This security measure creates a computational prohibitive barrier for attackers, maintaining the protocol’s integrity.
“With STARKs over smaller fields, we have a problem: there are only about two billion possible values of r to choose from, and so an attacker wanting to make a fake proof need only try two billion times - a lot of work, but quite doable for a determined attacker!”
Practical implications
The Fast Reed-Solomon Interactive Oracle Proofs of Proximity (FRI) prove that a function is a polynomial of a certain degree and is a crucial aspect of Circle STARKs.
Introducing Circle FRI, an approach that maintains the integrity of the cryptographic process, Circle STARKs ensure that non-polynomial inputs fail the proof.
Circle STARKs offer more flexibility and versatility for efficient computational performance by utilizing small fields and this new mathematical structure.
https://vitalik.eth.limo/general/2024/07/23/circlestarks.html
Originally posted by totse2118 the legit way is just getting your research published in lots of smaller journals but I read lots of stuff from those and people dedicate their lives to it and pay for their own research out of pocket from money they make working and they invest a lot, time and money into these subjects for a chance that one gets big and they can get more funding
This guy was broke until his research and products became the backbone of an entire technological revolution but most people don't have any kind of value or relevant science all lined up for society to gobble up. I'm sure people that fuck with computer stuff or robotics have a leg up on a laser researcher or cancer researcher but you never know. Vaccinologists and disease researchers are probably raking in the big bucks for years to come now
https://scholar.google.com/citations?user=DLP9gTAAAAAJ&hl=fr
this guy is mostly famous for crypto stuff but what real technology people in the community care about is if they have more than just a corporate front, like real technology and it's not widely understood that Vitalek has published scientific papers about cryptography so what he says isn't complete bullshit unlike 99% of crypto people -
2024-07-24 at 10:12 PM UTCI disagree with this entirely.
-
2024-07-24 at 10:17 PM UTC
The most important trend in STARK protocol design over the last two years has been the switch to working over small fields. The earliest production implementations of STARKs worked over 256-bit fields - arithmetic modulo large numbers such as 21888…95617
- which made these protocols naturally compatible with verifying elliptic curve-based signatures, and made them easy to reason about. But this led to inefficiency: in most cases we don't actually have good ways to make use of these larger numbers, and so they ended up as mostly wasted space, and even more wasted computation, since arithmetic over 4x bigger numbers takes ~9x more computation time. To deal with this, STARKs have started working over smaller fields: first Goldilocks (modulus
) and then Mersenne31 and BabyBear (
and
, respectively).
This switch has already led to demonstrated massive improvements in proving speed, most notably Starkware being able to prove 620,000 Poseidon2 hashes per second on an M3 laptop. Particularly, this means that, provided we're willing to trust Poseidon2 as a hash function, one of the hardest parts of making an efficient ZK-EVM is effectively solved. But how do these techniques work, and how do cryptographic proofs, which typically require large numbers for security, get built over these fields? And how do these protocols compare to even more exotic constructions such as Binius? This post will explore some of these nuances, with a particular eye to a construction called Circle STARKs (implemented in Starkware's stwo, Polygon's plonky3, and my own implementation in (sort of) python), which has some unique properties designed to be compatible with the highly efficient Mersenne31 field
Recent changes in the STARK protocol (a type of technology used in crypto) have made it much faster and more efficient. This is important because it makes crypto technology more practical and useful for everyday applications, potentially leading to its widespread adoption in the future.
Detailed Breakdown:
Old Method:
STARKs originally used very large numbers (256-bit fields) for their calculations.
These large numbers were useful for certain tasks (like verifying digital signatures) but were generally inefficient.
Using these large numbers meant more space was used and more computing power was needed, making the process slow.
New Method:
Recently, STARKs have switched to using smaller numbers (smaller fields).
Examples of these smaller fields include Goldilocks, Mersenne31, and BabyBear.
This change has made the process much faster without compromising security.
Proven Benefits:
The switch to smaller fields has significantly improved the speed of proving computations.
For instance, Starkware can now prove 620,000 hashes per second on a standard laptop, a task that was much slower before. -
2024-07-24 at 10:27 PM UTC
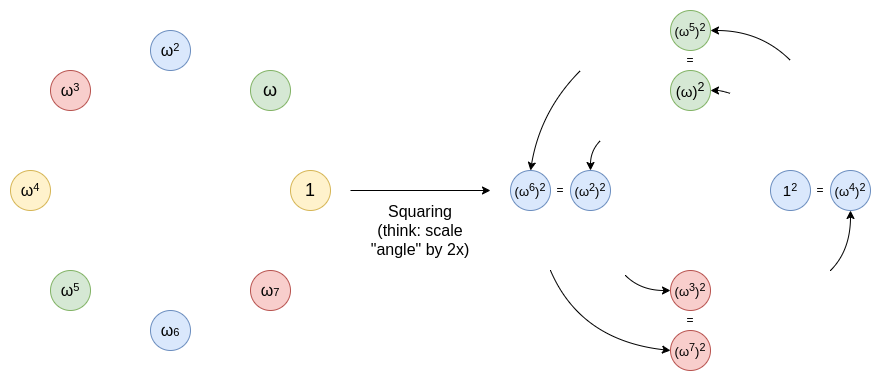
Conclusion: what do I think about circle STARKs?
Circle STARKs don't impose too many extra complexities on developers compared to regular STARKs. In the process of making an implementation, the above three issues are essentially the only differences that I saw compared to regular FRI. The underlying math behind what the "polynomials" that circle FRI is operating on is quite counterintuitive, and takes a while to understand and appreciate. But it just so happens that this complexity is hidden away in such a way it's not that visible to developers. The complexity of circle math is encapsulated, not systemic.
Understanding circle FRI and circle FFTs can also be a good intellectual gateway to understanding other "exotic FFTs": most notably binary-field FFTs as used in Binius and in LibSTARK before, and also spookier constructions such as elliptic curve FFTs, which use few-to-1 maps that work nicely with elliptic curve point operations.
With the combination of Mersenne31, BabyBear, and binary-field techniques like Binius, it does feel like we are approaching the limits of efficiency of the "base layer" of STARKs. At this point, I am expecting the frontiers of STARK optimization to move to making maximally-efficient arithmetizations of primitives like hash functions and signatures (and optimizing those primitives themselves for that purpose), making recursive constructions to enable more parallelization, arithmetizing VMs to improve developer experience, and other higher-level tasks
Faster hashing means that cryptographic operations, such as validating transactions and securing data, can be done more quickly. This improves the overall speed and efficiency of blockchain networks.
Enhanced Security:
High-speed hashing allows for more complex cryptographic functions to be performed in a reasonable amount of time, increasing the security of blockchain systems.
Scalability:
As blockchain networks grow, the ability to handle a large number of transactions quickly becomes crucial. High-speed hashing helps blockchains scale effectively, supporting more users and transactions without compromising performance.
Cost Reduction:
Faster computations reduce the need for expensive hardware and energy consumption, making blockchain technology more accessible and environmentally friendly.
Practical Applications:
Efficient hashing enables the development of more sophisticated decentralized applications (dApps) and services, expanding the use cases for blockchain technology beyond cryptocurrencies to areas like supply chain management, healthcare, and finance.
The advancements in STARKs, including Circle STARKs, are pushing the boundaries of what blockchain technology can achieve, potentially making it a superior alternative to traditional financial systems like SWIFT. This positions blockchain as a powerful tool for the future of money and technology, capable of transforming various industries and enabling new possibilities. -
2024-07-24 at 10:30 PM UTCyeah that's what I mean, all off
-
2024-07-24 at 10:35 PM UTCIs this all a big ETH 2.0 post merge ponzi scam or the future of technology folx?
https://www.binance.com/en/square/post/11191084796714Ethereum creator Vitalik Buterin is back again with another creation he believes will take blockchain’s security to a whole new level. He calls it Circle STARKS, and I’m here to tell you everything you need to know about it. Small fields changed the game
Circle STARKs is all about moving away from big, inefficient numbers to smaller, more manageable fields. Originally, STARKs used large 256-bit fields, but these were slow and wasted a lot of space. Now, with smaller fields like Goldilocks, Mersenne31, and BabyBear, everything runs faster and more efficiently. Starkware, for instance, can now handle 620,000 Poseidon2 hashes per second on an M3 laptop.
Vitalik’s Circle STARKs, implemented in Starkware’s stwo and Polygon’s plonky3, offer unique solutions using the Mersenne31 field. One of the main tricks in making hash-based proofs, or any proof, is to prove something about a polynomial by evaluating it at a random point.
For example, if a proof system needs you to commit to a polynomial P(x), you might need to show P(z) = 0 for a random point z. This is simpler than proving things directly about P(x). If you know z in advance, you could cheat by making P(x) fit that point. To stop this, z is chosen after the polynomial is provided, often by hashing the polynomial.
It works fine with large fields, like in elliptic curve protocols, but small fields pose a problem. With small fields, an attacker could just try all possible values for z, making it much easier to cheat. To solve this, two main methods are used: multiple random checks and extension fields. The first is simple—check the polynomial at several points instead of just one. But this can get inefficient quickly.
The second method, using extension fields, involves creating new, complex numbers that make it harder to guess z.
………………………….
To handle this, Circle STARKs use interpolants—functions that equal zero at two points. By subtracting and dividing by these interpolants, you can show that the resulting quotient is a polynomial.
Vanishing polynomials, which equal zero across an evaluation domain, also play a role. In regular STARKs, this is straightforward. In Circle STARKs, it involves repeating specific functions, which makes sure the math holds up.
As Vitalik puts it, “The complexity of circle math is encapsulated, not systemic.”
I am not a big maths guy i'll be honest buy according to AI"The complexity of circle math is encapsulated, not systemic" means that the intricate and complicated mathematical operations involved in circle STARKs are contained within specific parts of the system and do not affect the entire system.
In practical terms, this means that developers can build and work with circle STARKs without needing to grasp the complicated underlying mathematics. The system is designed in such a way that the tough math is taken care of internally, allowing developers to focus on building applications and functionalities. -
2024-07-24 at 10:47 PM UTCFrom what I understand what's going on here is instead of typical PoW crypto blockchain ecosystems where computers are spending energy to "mine a block" aka compute a correct number, but in the ETH PoS ecosystem instead of the network being based off this computers rolling blocks instead the hashes are being rolled against hashes in an endless loop expanding infinite scalable circle of this giant network
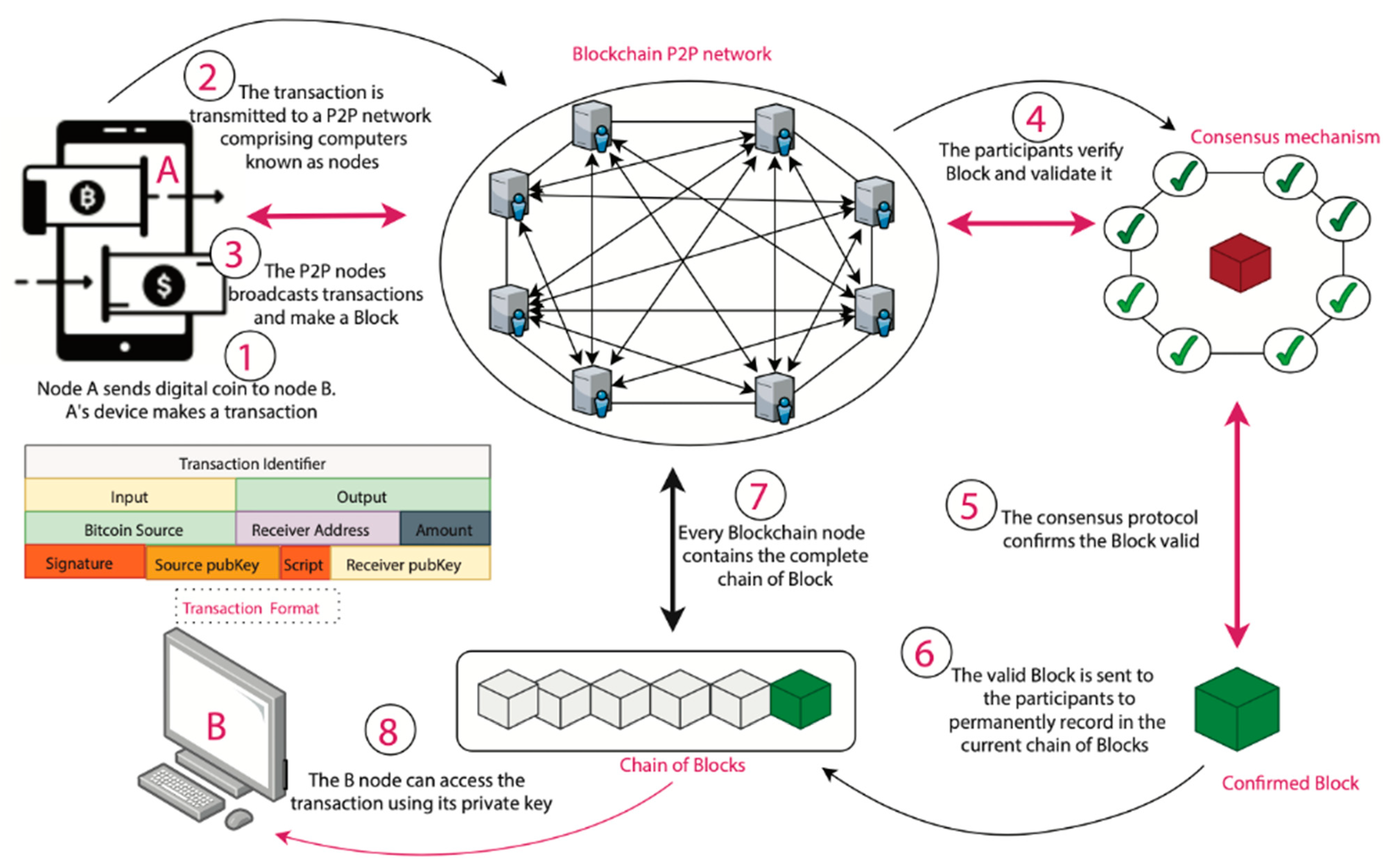
so basically instead of mining a block you are solving a hash and that hash is verifying another hash, which verifies another hash, etc etc x1000 and when the computer says "okay this is legit" then it starts "mining the block" and each of these transactions takes 0.01% of network power and all take place 60,000 times per second per computer so I can see how this would be more scalable and secure than say a 52% bitcoin network attack but are micro polynomial improvements over hashing really that much of an improvement from the bitcoin lightning network which basically does the same thing?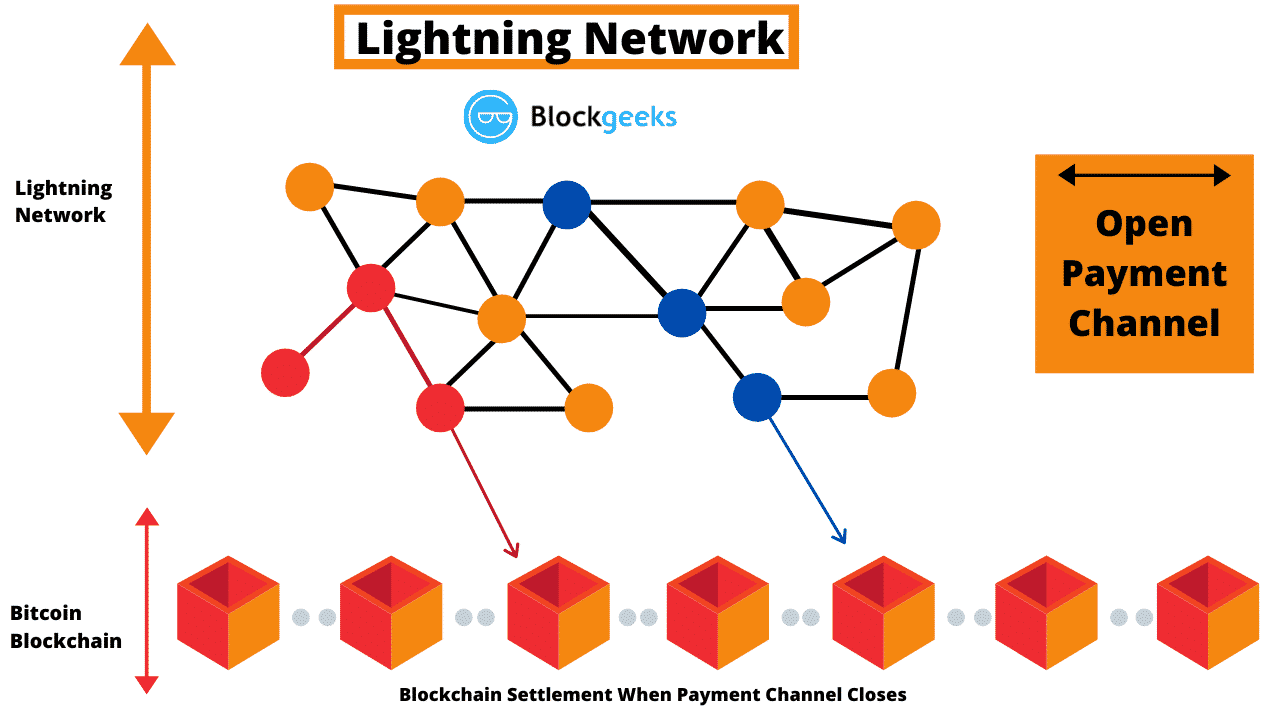
https://bitcoinmagazine.com/technical/lightning-network-payment-technology-advantages
ETH PoS network is more based on computational power i.e staked ETH which = bigger pool payouts but the bitcoin lightning network is more "fee based" with each node representing a miner trying to solve a block VS a pool of ETH locked in a network